GERAK HARMONIK TEREDAM PEGAS DALAM ZAT CAIR
Nasri Nasriah
Laboratoriun Fisika komputasi II
Fakultas Sains dan Teknologi
Universitas Islam Negeri Sunan Gunung Djati Bandung
Jl. A.H. Nasution No. 105 Cibiru Bandung 40614
22 September 2011
Abstrak
Gerak harmonik adalah gerak yang terjadi secara berulang pada selang waktu tertentu. Gerak harmonik dapat dibedakan menjadi empat yaitu gerak harmonik tak teredam, gerak harmonik teredam berosilasi (underdamped), gerak harmonik teredam kritis (critically damped), dan gerak harmonik teredam jenuh (overdamped). Percobaan ini membuktikan bahwa grafik yang dihasilkan antara hasil teori dan hasil matlab ternyata sama. Sesuai dengan teori dan hasil matlab yang memiliki nilai konstanta redaman yang paling kecil yaitu gerak harmonik teredam berosilasi (underdamped) dan yang memiliki nilai konstanta redaman paling besar adalah gerak harmonik teredam jenuh (overdamped).
Kata kunci: Gerak harmonik, underdamped, critically damped, overdmped.
I. Pendahuluan
1.1. Latar belakang
Disetiap hari dunia mengalami perkembangan, begitu pun dibidang fisika terutama fisika komputasi yang semakin hari semakin berkembang. Dalam perkembangan ini fisika komputasi berpengaruh sekali dalam kehidupan sehari-hari untuk aplikasi pengkomputasian yang akan membantu memperingan tugas manusia. Pada percobaan kali ini dalam fisika komputasi mencoba untuk mengkomputasikan gerak harmonik tak teredam, gerak harmonik teredam berosilasi, gerak harmonik yang teredam kritis dan gerak harmonik yang teredam jenuh. Dalam pengkomputasian ini membantu memperingan atau mempermudah dalam membuat grafik dan menghitung nilai yang dihasilkan pada gerak harmonik.
1.2. Tujuan
· Mengetahui cara mengoperasikan dan prosedur membuat program dasar dalam MATLAB pada gerak harmonik
· Mengetahui cara menginisialisasi variable dalam MATLAB pada gerak harmonik
· Mengetahui operasi matematika dan fungsi dasar dalam MATLAB pada gerak harmonik
· Mengetahui cara membuat grafik pada MATLAB pada gerak harmonik
1.3. Tinjauan pustaka
Setiap gerak yang terjadi secara berulang dalam selang waktu yang sama disebut gerak periodik. Karena gerak ini terjadi secara teratur maka disebut juga sebagai gerak harmonik/harmonis. Apabila suatu partikel melakukan gerak periodik pada lintasan yang sama maka geraknya disebut gerak osilasi/ getaran. Bentuk yang sederhana dari gerak periodik adalah benda yang berosilasi pada ujung pegas. Karenanya kita menyebutnya gerak harmonis sederhana. Banyak jenis gerak lain (osilasi dawai, roda keseimbangan arloji, atom dalam molekul, dan sebagainya) yang mirip dengan jenis gerakan ini, sehingga pada kesempatan ini kita akan membahasnya secara mendetail.
Dalam kehidupan sehari-hari, gerak bolak balik benda yang bergetar terjadi tidak tepat sama karena pengaruh gaya gesekan. Ketika kita memainkan gitar, senar gitar tersebut akan berhenti bergetar apabila kita menghentikan petikan. Demikian juga bandul yang berhenti berayun jika tidak digerakan secara berulang. Hal ini disebabkan karena adanya gaya gesekan. Gaya gesekan menyebabkan benda-benda tersebut berhenti berosilasi. Jenis getaran seperti ini disebut getaran harmonik teredam. Walaupun kita tidak dapat menghindari gesekan, kita dapat meniadakan efek redaman dengan menambahkan energi ke dalam sistem yang berosilasi untuk mengisi kembali energi yang hilang akibat gesekan, salah satu contohnya adalah pegas dalam arloji yang sering kita pakai. Pada kesempatan ini kita hanya membahas gerak harmonik sederhana secara mendetail, karena dalam kehidupan sehari-hari terdapat banyak jenis gerak yang menyerupai sistem ini.
Gerak osilasi terjadi bila sebuah sistem diganggu dari posisi kesetimbangan stabilnya.
Karakteristik gerak osilasi yang paling dikenal adalah gerak tersebut bersifat periodik yaitu berulang-ulang. Banyak contoh osilasi yang mudah dikenali, misalnya perahu kecil yang berayun turun naik, bandul jam yang berayun ke kiri dan ke kanan, dan osilasi molekul udara dalam gelombang bunyi.
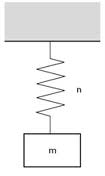
Satu macam gerak osilasi yang lazim dan sangat penting adalah gerak harmonik sederhana. Apabila sebuah benda disimpangkan dari kedudukan setimbangnya, gerak harmonik sederhana akan terjadi seandainya ada gaya pemulih yang sebanding dengan simpangan dan kesetimbangannya kecil. Suatu sistem yang menunjukan gerak harmonik sederhana adalah sebuah benda yang tertambat ke sebuah pegas secara vertikal.
Gambar: Sistem pegas vertikal gerak harmonik sederhana.
Gambar: Sistem pegas vertikal gerak harmonik sederhana.
Pada keadaan setimbang, pegas tidak mengerjakan gaya pada benda. Apabila benda disimpangkan sejauh y dari kedudukan setimbangnya, pegas mengerjakan gaya –ky ,dan terdapat gaya mg ke bawah seperti yang diberikan oleh hukum Hook:
Fy = - ky
Tanda minus pada hukum Hook timbul karena gaya pegas ini berlawanan arah dengan simpangan. Jika kita memilih y positif untuk simpangan ke bawah maka y negatif terjadi jika simpangan ke atas. Dengan menggabungkan hukum Hook dengan persamaan hukum Newton maka akan didapatkan:
Fy = - ky + mg
Percepatan berbanding lurus dan arahnya berlawanan dengan simpangan. Hal ini merupakan karakteristik umum gerak harmonik sederhana dan bahkan dapat digunakan untuk mengidentifikasi sistem-sistem yang dapat menunjukan gejala gerak harmonik sederhana. Adapun gerak harmonik diklasifikasikan lagi menjadi dua jenis yaitu gerak harmonik teredam dan gerak harmonik tak teredam yang mana klasifikasi ini didasarkan pada ada tidaknya gaya gesek yang mempengaruhi gerak osilasi benda.
Pada semua gerakan osilasi yang sebenarnya energi mekanik terdisipasi karena adanya suatu gaya gesekan. Bila dibiarkan saja amplitudo dari gerakannya akan semakin berkurang hingga akhirnya nol yang menyebabkan benda berhenti bergerak. Bila energi mekanik gerak osilasi berkurang terhadap waktu, gerak dikatakan teredam. Jika gaya gesekan atau redaman kecil gerak hampir periodik sekalipun amplitudo berkurang secara lambat terhadap waktu. Selain adanya gaya balik pada gerak ini ada gaya lain yang bekerja melawan arah gerak misalnya karena kekentalan zat cair atau bidang yang tak licin, tempat gerakan berlangsung.
Misal gaya seperti ini adalah F = -rv dengan r adalah konstanta redaman dan v faktor kecepatan. Tanda negatif menunjukan bahwa gaya ini berlawanan dengan arah gerak. Persamaan gerak yang terjadi adalah:
∑F = - kx – rv = ma
Jika redaman sangat besar, lebih besar dari dan menjadi imaginer. Disini tak ada osilasi dan simpangan benda akan menjadi nol tanpa melewati kedudukan setimbangnya paling tidak akan melewati kedudukan setimbang satu kali.
Macam – macam gerak harmonik teredam:
1. r = 0, tak teredam
2. r < akar 4km, gerak harmonik yang “underdamped” (teredam berosilasi).
3. r = 4km, gerak harmonik yang “critically damped” (teredam kritis) osilasi berhenti, kedudukan setimbang dicapai dalam waktu singkat.
4. r > akar 4km, gerak harmonik yang “overdamped”(teredam jenuh) kedudukan setimbang dicapai dalam waktu lama.
II. Metode Eksperimen
2.1. Waktu dan tempat
Hari/Tanggal : Kamis, 22 September 2011
Waktu : 10.30 – 12.00 WIB
Tempat : Laboratorium Fisika Komputasi 2, Sains dan Teknologi
UIN Sunan Gunung Djati Bandung
2.2. Alat dan bahan
· Laptop
· Program matlab
2.3. Prosedur kerja
Simulasi dengan matlab : langkah pertama adalah menentukan besaran yang diketahui nilainya, kemudian menuliskan rumus yang akan digunakan, setelah itu membuat grafik posisi x terhadap waktu t pada matlab, dengan empat kondisi yaitu tak teredam, under damped, critically damped, dan overdamped.
III. Hasil dan Pembahasan
2.5. Pembahasan
Berdasarkan simulasi dimatlab grafik yang dihasilkan sesuai dengan teori. Pada grafik yang pertama yaitu pada gerak osilasi tak teredam grafik yang dihasilkan sinusoidal dan tidak ada pelemahan pada osilasinya atau simpangannya sama ditiap sekon dapat dikatakan juga simpangan yang dihasilkan itu konstan dan itu berarti nilai konstanta redamannya sama dengan nol. Sedangkan pada grafik yang kedua yaitu gerak harmonik yang teredam berosilasi grafik yang dihasilkan memiliki simpangan lebih kecil dari pada gerak harmonik tak teredam dan simpangan yang dihasilkan tidak sama disetiap waktunya atau dapat dikatakan pada gerak harmonik yang teredam berosilasi ini memiliki nilai konstatnta redaman, dan dari grafik di peroleh semakin lama waktu yang dibutuhkan maka simpangan yang dihasilkan pun semakin kecil atau melemah. Sedangkan pada grafik ketiga dan keempat yaitu pada gerak harmonik yang teredam kritis dan gerak harmonik yang teredam jenuh memiliki simpangan yang hampir sama dengan gerak harmonik yang teredam berosilasi yaitu semakin lama waktu yang dibutuhkan maka simpangan yang dihasilkan akan semakin kecil dan melemah dan bahkan dikondisi tertentu gerak osilasi ini tidak menghasilkan simpangan dan pada konstanta redamannya pun memiliki nilai. Tetapi pada keempat gerak osilasi yang teredam ini masing-masing memiliki perbedaan. Perbedaan ini dilihat dari nilai simpangan yang dihasilkan pada saat osilasi sesuai dengan teori. Gerak osilasi harmonik yang memiliki nilai simpangan paling kecil yaitu gerak osilasi harmonik tak teredam karena pada gerak osilasi tak teredam ini memiliki nilai konstanta redaman yang sama dengan nol. Sedangkan gerak harmonik yang teredam berosilasi (underdamped) memiliki nilai konstanta redaman r < . Dan untuk gerak harmonik yang teredam kritis (critically damped) memiliki nilai redaman r = 4km. Dan yang terakhir gerak harmonik yang teredam jenuh (overdamped) memiliki nilai redaman r > akar 4km . Berdasarkan grafik jika dibandingkan gerak harmonik teredam yang memiliki nilai konstanta redaman paling kecil adalah gerak harmonik yang teredam berosilasi (underdamped) dan yang memiliki nilai konstanta redaman paling besar adalah gerak harmonik yang teredam jenuh (overdamped).
IV. Penutup
4.1. Kesimpulan
Dengan percobaan ini dapat diketahui bagaimana meng-komputasikan gerak harmonik sederhana dimatlab baik yang teredam maupun yang tak teredam. Hasil pengkomputasian pada matlab ternyata sesuai dengan teori yang sudah ada yaitu pada gerak osilasi tak teredam simpangannya tidak berkurang atau tidak melemah. Sedangka pada gerak osilasi yang teredam memiliki simpangan yang berkurang atau melemah. Pada simpangan gerak osilasi yang teredam yang memiliki nilai konstanta redaman paling kecil yaitu gerak harmonik yang teredam berosilasi (underdamped) dan yang memiliki nilai konstanta redaman paling besar adalah gerak harmonik yang teredam jenuh (overdamped). Dan dapat dikatakan hasilnya sama dengan teori.
4.2. Saran
Dalam percobaan ini sebaiknya lebih teliti lagi dalam menggunakan matlab terutama dalam menuliskan rumus-rumus dan lambang yang akan digunakan.
Daftar Pustaka
· Sanjaya, Mada. 2011. Komputasi Fisika Berbasis Matlab. Bandung.



Tidak ada komentar:
Posting Komentar